Pandemic pensees

​Time is tight

Some readers of a certain age will remember Booker T and the MGs and their music. Time is tight (1969) was regularly played in the discos when I was a teenager, old enough to go out.

Time is tight is a useful mantra, though, in education, because everything is time limited, lessons, days, weeks, terms and now, after children have missed several weeks of personal contact with teachers, but having worked remotely for that time, with mixed outcomes, some commentators are looking at the situation and making statements about lost education. We don’t know how long this current situation will last.

Whatever we might wish, children will eventually arrive back in school “where they are”. Some will have kept up. Some will potentially be ahead of where teachers were expecting them to be and some will have less secure progress, with a few significantly concerning. There will be a need to establish where each child is and to determine the best way forward.

It will need an integrated approach and a reflection on learning dynamics, the link between school and home, of catch-up is to have any effect.

In Primary, this is likely to focus on maths and English. It might be possible now, having used remote learning for several weeks, to look at the dynamics of learning, to have a clearer focus on independent home tasking, maybe using home for practice tasks, with classroom looking at the teaching and addressing of evident misconceptions, with specific guidance for individuals.

It might be feasible for reading aloud, as a form of self-check, to be submitted through IT, using a phone, tablet or laptop as the receiver, to be forwarded to the school.

Extended writing could be done at home, following in-lesson stimulus and planning, with drafts coming back for reflective discussion.

In this way, I could see less argument for holiday schooling, as being proposed by some commentators. At this point in the pandemic, we cannot be secure in making any plans for a return to “normal school”.

Time with a known teacher is far more productive than time with a stranger, and I use the word stranger advisedly. Essential DBS checks on any army of volunteers, even retired teachers, could stretch some of the current systems.

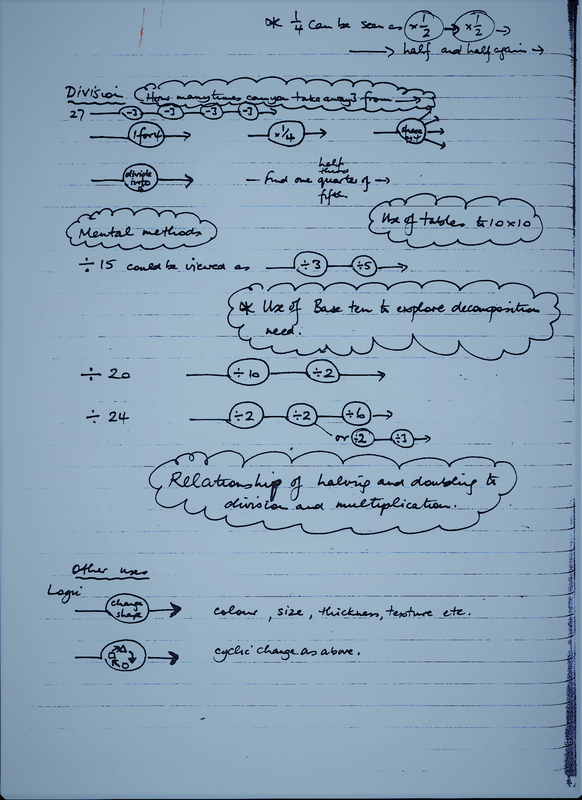
Children will have missed a few topics. Deciding whether these are “essential”, given forthcoming plans might determine a few tweaks. If an essential topic is to replace another, by definition less essential topic, a further consideration might be to look at the allocation of time to the topic. Does the essential topic need to take, say, seven weeks of a half term, or could it be covered in five, leaving two weeks to offer a taster of the less essential topic? Moving away from the half term topic would free time.

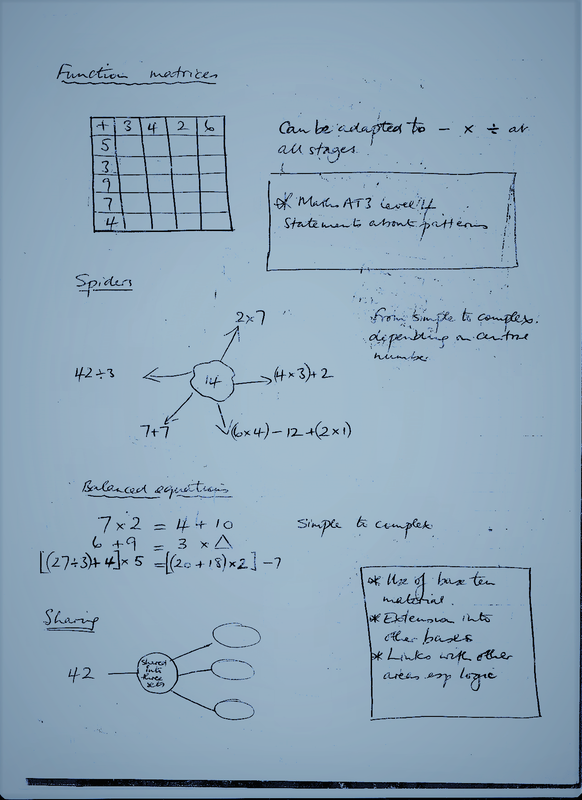
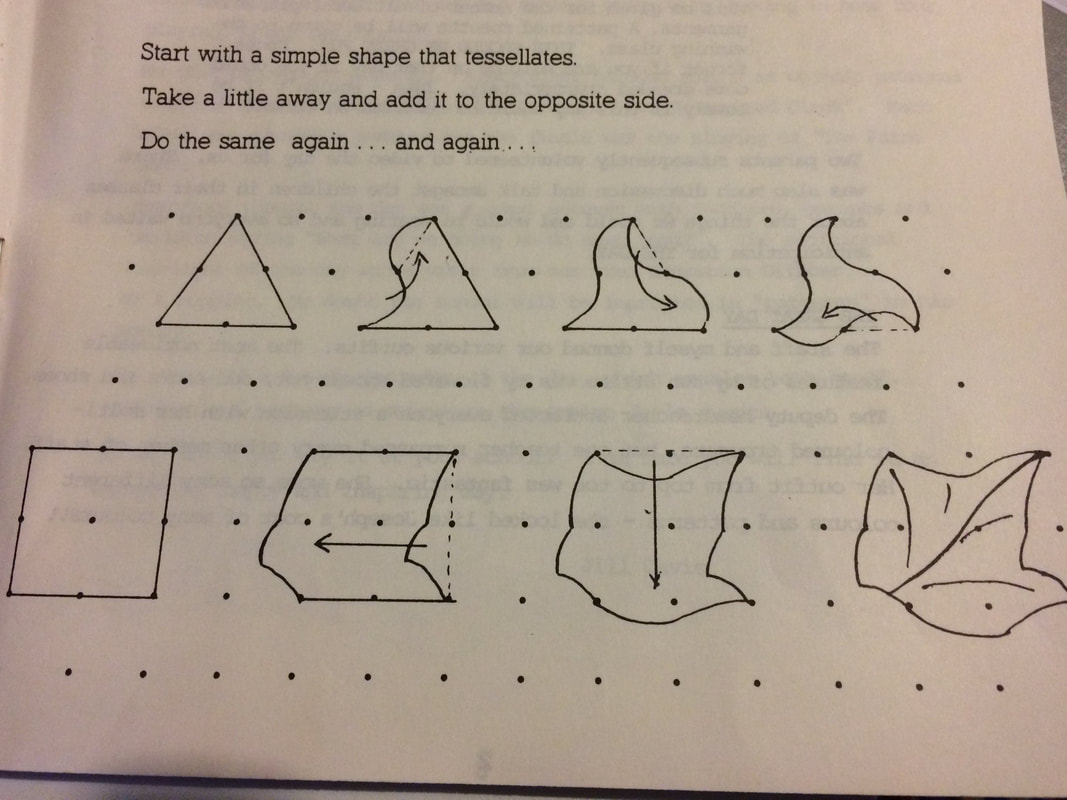
All topics lend themselves to supporting the English and often maths curriculum, especially talking, reading and different writing forms, counting, leading to data and measures.

Integrating the different elements can help to free some time. How about sending home a piece of text to read, or an image to consider before a subsequent discussion lesson? Why spend fifteen minutes of a lesson giving time for consideration? Use the time to collate and share responses.

Space, time and resources are in teacher control. How they are used to support learning are under teacher direction. Time management will become more pressing as time passes.

Time is tight; to be used with care.

 
Field geometry?

Looking for simple challenges for children to use outdoors that have links to wider learning, straight lines and circles come to mind.

Challenges:

Lines
Using only three poles and either chalk or cones, can you create a straight line between two points on the playground or field?

Lines can be extended to drawing other geometric shapes. How about exploring Pythagoras theorem? It’s possible with year six. Linking squares with triangles and maybe extending to right angles and building with such simple geometry; builders 3,4,5 triangle?

Can you devise a method for drawing a vertical line? Crib note plumb line, a weight on a string.

Circles
You have a piece of string and a piece of chalk. Devise a way to draw a circle on the playground; for older children, that has a radius of 50cm.

What happens if you have drawn a circle, then “walked” the chalk radius around the circumference and marked points? What shape would it make? How else can a circle be divided?
​
What happens if you draw a straight line, then draw circles at 20cm points along the line? Play with shapes?  
All these challenges could be replicated on a smaller scale with a compass, a ruler and pencils, exploring shapes within circles.

Make windmills?
This exercise was a part of a topic that I did around 1984, with a year six class, looking at energy, so it has some current resonance. Wind and water energies were exemplified and explored through a visit to a local windmill and watermill. Within the DT curriculum, attempts were made to create working models.

Alongside that, exploring circles allowed a homework project to create wind “turbines” that became the focus for a fair test to find the most efficient. The testing was relatively simple, with each turbine mounted on a compass, on a pencil embedded in the ground.
​
Of course, just making our own windmill, coloured in, could be an interesting task in itself.
​

With schools looking carefully at ways to accommodate children back into school, then with the advice/guidance to do as much working outside as possible, I thought I would put together a collection of ideas that might offer some start points, together with links to other blogs on my site that could add further.

The external environment can enable some high-quality opportunities for underpinning and understanding the use and application of the knowledge that is learned in the classroom.

Sensory experience is the beginning of exploration. Seeing, listening, touching, smelling and tasting, appropriately, are all essential basics. https://chrischiversthinks.weebly.com/blog-thinking-aloud/five-senses-starter

In English, for example, exploration of the site for micro-settings can be the starter for perhaps putting figures into the environment, creating an adventure in the micro world. If children are able to lie down and see that micro world from the point of view of the character, they can place themselves into the adventure. Really adventurous opportunities could be taken to fully storyboard and script the adventure, it could be created as an animated film.

Descriptive opportunities are all around; everything is capable of description, orally or in writing.

Report writing is also supported by outside activity, maybe in the form of a daily diary, a summative description of a specific event or activity. Rules or instructions for games being played?

Art. In the same way everything can be drawn, or painted or photographed, for use as the basis for a larger piece of work, which might be collage. How about incorporating natural materials? Don’t forget to encourage the exploration of colour naming, too. How about giving out a colour chart and getting children to find an object of each colour?

Looking at maths, counting opportunities are everywhere. How many… bricks in a metre square? How many bricks high is the school? How many paving stones in a patio? Ow broad are tree canopies? What is the circumference of a tree? Work out the diameter?

How many… petals on a daisy? This is interesting. Do all daisies have the same number of petals? Each child to pick ten, to organise and count each one. Results collated in a group, as a bar chart.

Measures. How long is… this can lead to measuring all aspects of the school, put onto a sketch map, with older children then transposing the measurements into a scale drawing of the school.
​
Angles, yr 6, could be incorporated into the measures activity, as a form of triangulation activity, perhaps using a 360 degree protractor with a pointer fixed to the centre. Heights of things, buildings or trees, could be calculated from an activity using a clinometer, an angle metre. Don’t forget to remind the children about their own height, to their eyes…
​

Activity data, link with PE; one minute data, see this blog… https://chrischiversthinks.weebly.com/blog-thinking-aloud/quick-one-minute-data

Having explored mapping the site, as a Geography activity, looking at the micro sites for ecology is a very useful activity. Go out onto the/a “grass” area. How many different plants actually make up the “grass” area? With a tray, childnre to look for and collect examples of different leaves of plants, to then seek to identify. Are there areas where plants are left uncut? How does this affect the growing paterns of the same plants? How high do they grow, uncut? How low can daisies flower?

 Animal tracks and signs can be surprising. What lives in the school grounds and what evidence is there that they are round? Blog, with pictures. https://chrischiversthinks.weebly.com/blog-thinking-aloud/creating-nature-detectives

Minibeasts. How about hunting the Triantiwontigongolope? Poem, song and ideas for minibeast hunting… https://chrischiversthinks.weebly.com/blog-thinking-aloud/triantiwontigongolope

Creating observers of the world is a key starting point for further exploration, in that it enables questions, from either the child or the teacher. All questions can be followed up. https://chrischiversthinks.weebly.com/blog-thinking-aloud/observation-get-them-to-look
​
The deepening of exploration can be calibrated through a structured questining scaffold, as per the diagram below.

The material world of the school can be explored, looking at the building architectural features; what holds it up, what different materials have been used, for what purposes? Materials outside? What’s the soil made from? Anything looked at can be enhanced through a magnifier, or possibly under a visualiser on the IWB.

Are there shadows in the school grounds? How about making a sundial to check on the movement and maybe make a clock? How do shadows change in length at different times of the day? Why?

If it rains on a day when the sun may come out. How about drawing around a puddle and seeing how it alters during the day?

Using the sun to explore the drying action on different materials? Which material dries the fastest, or slowest?

Primary science is about children
Asking questions
About their real world
And
Finding answers by some kind of first-hand experience.
It is about children being scientific,
A process involving the skills of

Observing; starting with direct and short term observations,
Employing all their senses
And later,
Using tools to aid the senses to find the less obvious
And increase their ability to select from those observations
Those things that are meaningful,
Later ordering those observations to derive pattern and structure

Classifying; beginning by sorting things
According to attributes selected by the children,
Recognising similarities and differences,
Gradually accepting and using official ways of classifying.

Measuring; using non-standard units of volume, time, length, mass,
Later moving to standard measures, with increasing accuracy
And more sophisticated instruments.
Using measures to determine patterns of events, such as growth and change.

Predicting; speculating about possible outcomes of events or experiments,
At first intuitively,
Later making use of prior experience and logical argument,
To develop predictions that can be tested by experiment,
Eventually being able to formulate general hypotheses
Rather than single predictions.

Experimenting; early attempts to make tests fair
And record results,
Takin increasing care over control of variables,
Later selecting specialised equipment to tackle practical problems
That are abstract from familiar environments.

Communicating; Oral and drawn descriptions of first hand experiences,
Late developing a more precise use of language of planning, reporting and explaining,
Events or experiments,
Increasingly more accurate in recording,
Developing diagrams, graphs and working with data,
Making general statements, conclusions, from the results.

Explaining; exploring the links between cause and effect,
When I did this…that happened,
With increasing use of reference material
Supporting their thinking and reflections,
Later developing explanations that derive from their reflections
Rather than relying on first-hand experience.

Evaluating; reflecting on the whole process,
Suggesting ways in which they would change their approach,
Next time.

Making sense of their experiences, through refining and honing central skills,
Using developing knowledge to help address new situations…

​
On my blog, in the contents section, scroll down towards the bottom to find more subject ideas.  https://chrischiversthinks.weebly.com/contents.html
​

Pandemic pensées
We’re living in very strange times. The world’s closed down. People are at home, some working, some furloughed, some looking after themselves or others, whose lives may be risked by catching the current virus.
Teachers are working really hard to maintain some elements of normality among the altered reality and, in different households, the capacity to support children with any areas of learning might be strained. Teacher capacity to identify and support individuals with specific help will also be constrained.
Children have been put into a situation where they are distance learning. Even as an adult, this can be a challenge, in motivation, resourcefulness and perseverance. Frustrations that might be expressed in normal times about “not understanding” what is expected may be exaggerated further by the expectations of a number of hours each day devoted to “schoolwork”.
This tweet, posted by an Aussie teacher made me stop and think.
​

Teachers may well be sending home work that challenges the child’s ability to conceptualise what is being expected. If we look at maths as a separate area, in this case, a teacher or other adult might seek to unpick the problem and exemplify what is being asked by the use of supportive diagrams or with reference to physical materials.
But… home is not school, so the resources may not be available.
That, in itself, set off a train of thought and took me back to my first classroom, which I inherited with resources that were either twenty years old, or non-existent. There was a need to create, devise or collect resources that would support counting, matching and grouping. So visits to the beach might mean picking up shells to bring home, boil and clean to take into school. Autumn meant collecting conkers. I did try marbles, at one time, but, for some reason, they kept going missing… It soon became clear that anything could become a counting aid, so newsletter requests to parents helped with a variety of materials and the local sweet shop was a source of large, clear jars.
I thought it might be an idea to consider how to make resources from very simple materials that might be available in homes, provide useful activities in their development, then be useful in specific maths activities.
Let’s start with counting.
It’s possible that families are getting through quite a lot of cereal, or other boxed foods. The cardboard can be used as free base materials. A ruler, marker pen, pencil and scissors are needed.

Open out the boxes and cut the larger pieces. Keep bits, in case you want to make more at some stage.
​

Measure and rule a 1cm grid, or larger, 2cm, if you are worried for a child’s dexterity, using as much of the card as possible. Identify a couple of 10*10 grids, as 100 squares, where you can cut 10 squares into “rods”, leaving the remainder to become “ones”, “singles” or “units”.

Drawing a 3cm by 4cm grid can create a series of rectangles that become number cards. If you have enough, numbering to 100 is very useful to challenge later learning.
​

Cut out the various pieces.
​

Combining the counting numbers with the cut out counters can begin to develop thinking mathematically, matching numbers, showing these in physical form.

Challenges can then develop, linking physical, diagrammatic and abstract.
​

A very simple activity that can be very effective in supporting rapid calculation could be called race to or from the flat. This can be an extension from making the resources above, with the addition of one or more dice.
​

As long as you have made the materials above and have some dice, this can be developed to cater for a variety of needs.

The rules of each game are simply described.
​
·         Decide whether it’s a race to or from the flat (100 square). Decide whether, when the dice are thrown, the numbers are added together (any number of dice) or multiplied (two or three dice?).
·         Dienes materials available tin the centre of players, plus dice appropriate to the needs of the group.
·         Each child takes turns to throw the dice and calculate the sum or product.
·         This amount is then taken from the general pile and placed in front of the child. The calculation can be recorded eg 3+4=7. This can provide a second layer of checking.
·         If playing race from the flat, the child starts with ten ten rods, then takes an appropriate amount from these.
·         Subsequent rounds see pieces added to the child’s collection; recorded as needed, eg round 2, 5+2=7 (7+7=14; the teacher should see one ten and four ones)
·         The first child to or from the flat is the winner.


Altering the number of dice alters the challenge.

It’s interesting having a perspective on working in education and learning that now spans 48 years from walking into Training College. There have been many changes and challenges along the way, but, in essence, there is much more in common across the ages than difference.

Let’s start at the very beginning
A very good place to start.
When you read you begin with ABC
Let's see if I can make it easier

As a parent of three, step-parent to three and a grandparent to eight, I have had a lot of opportunities to view children growing up; the current span is from 15 months to almost 15 years. Each of the family settings varies, in place, parental jobs and therefore available time and in disposable incomes. These variables inevitably play some part in the opportunities that are available to each family and therefore on the cultural potential made available to each child.

The children grow and flourish through their parental love, diet and their spoken language, with appropriate encouragement to make marks and to enjoy books.

The environment that surrounds young children today is different from that which I enjoyed. Not in terms of the natural world, where there are still plants, animals and natural features; in some cases just… but perhaps their opportunity to engage with it, with an interested adult able to point out the different elements and to provide the names of things. There are also the distractions of the digital world. Whereas as a child, I was more au fait with string and a penknife and den making, today’s young have early access to screen distractions and can very soon work their way into desired apps.

I have long worried that a school cannot rely on a child’s ability to identify easily with the elements of their locality to support their speaking, their reading and their writing attempts. Having spent time as a volunteer, leading wildlife groups, it was clear in the 1980s that it was a minority interest. Education does still rely, to some extent on a child’s experience beyond the school gates.

How does a child describe the feeling of walking on sand in bare feet, paddling in the sea or lake, getting caught in a rain storm, walking through long grass, the sound of leaves being walked on or kicked, and so many other things, if they haven’t had the opportunity?

Can we build a strong curriculum and strong education on missing experiences? Is experience the beginning of “knowledge rich” education, in that it provides a base for things to “stick” to?

What’s school? People, places and things

Organise rooms, which used to be defined as 55 sq m for a group of 30 children, or a currently defined infant classful.
Supply desks and chairs; this has varied over time, with discussions about the amount of table space needed.

There’s also been wide variation on whether to supply personal storage space for books; should children be responsible for their own exercise books or should they be centralised? Either decision can cause logistical issues when books are needed for a lesson; either movement of each child to find their one book, or teacher/monitors to give out books. This can be pre-empted between lessons, getting out books on entry to the classroom, or someone must give them out before the lesson; assuming places are known…

Classroom resources need a retrieval and return system that can facilitate whole class lessons as well as intermittent needs; variation between age groups, from picture clues to written headings.

Space, resources and time have always been the variables within a school and teacher’s organisational control.

Space…

How much space is available to support the learners, and how is it orientated to support the teaching that is likely to happen?

How desks are arranged, to allow sight lines, ease of movement around the classroom, for children and adults, but also to facilitate different areas of the curriculum. Alteration to the needs of different subjects and teaching may need to be easily accomplished; I have seen whole classroom reorganisation within a couple of minutes, accompanied by a piece of music. “I can’t do x because of the way tables are arranged.” does not seem to me to be a reasonable response. Where there’s a will…

Resources…

Throughout my teaching career, there have been shelves of resources that have been bought at some stage, because they seemed a good idea at the time or because the sales patter was irresistible. They gathered dust through lack of use, often because newer staff were unaware of the potential of the resource. There’s a significant need to keep on top of learning resources, to ensure that they are up to date and do the job that’s required of them. Collated and identified, they are more likely to be used than if they are just in a pile somewhere.

There’s probably a similar kit of resources in every classroom, centred around the stationery, which also needs some organisation. Painted tins and glass jam jars were a feature of my first classroom. Today there’s a variety of plastic tool boxes (scissors, erasers rulers), cutlery drawers (paint brushes) or cutlery holders for pens and pencils. Classroom desks can also sometimes be awash with SPaG reminders, or similar prompts.

Maths, reading, writing, art corners might be created, as resource bases, with topic resources brought in to need, from a central collection.

Time…

It’s sometimes easy to forget that time in school is under teacher and school control, but, some organisational elements can exert control over the available time that puts pressure on lesson dynamics, especially for some vulnerable learners who can’t quite get things finished. If it’s clear that a child has worked hard, for them, and needs a bit of finishing time, does this mean part of a playtime lost, or can the teacher allow a few extra minutes in order for the child to finish?

We have been in a period where maths and English have seemed to dominate the curriculum. Some organisation of this, sets for example, impose a timetable need. This can mean that some children might not be able to access the learning in the available time, but, in a classroom setting, perhaps the teacher can make an executive decision to add a few necessary minutes to a lesson, to bridge a playtime and allow children some “finishing off time” rather than rushing and not completing or not being able to show their best efforts.

It’s also possible to find many examples where tasks/activities are chosen to fill the set time, rather than being able to challenge all children, limiting some.

School time is often extended through “homework”. At Primary, if homework is to be seen as a useful adjunct to school work, I would prefer to see talking homework, eg a question or an image to discuss, with the outcomes of discussion feeding back into lessons. Click on the blue title to open a linked blog.

 Primary Curriculum; a child’s world?

There have been great similarities across my career in the curriculum offerings of every school. For a start, there was always mathematics, more often than not supported by a bought scheme. The strictness of adherence to the scheme varied from school to school, but, in all cases, we were required to use the Teacher’s Guide as our methodological “bible”, to ensure consistency of approach.

English varied more from school to school, with the majority drawing heavily on the topic curriculum for stimuli for talk and writing. Reading, from around 1975 was supported by the Cliff Moon colour coded system, with different layers of books available to the children; one at teacher level, where there might be a small number of errors, and one at more fluent levels, to read in free time or at home, with or without a parent. Most of the schools in which I worked in the 70/80s also had a Home-School reading diary, with parents encouraged to record their thoughts from hearing their children read. It was very much individualised and we were encouraged to hear children read regularly. Writing was collated into excellent practice during the National Writing Project 1985-8. It mirrored what good schools were already doing, but also gave the basis for conversation between schools about what constituted good writing experiences.

Topic work enabled science, history and geography to lead investigation, with music, PE (dance), DT and art to be used to interpret the outcomes of the investigation. This element of the curriculum provided the opportunities for report writing, letters, note taking and a range of genres with imaginative narratives. The school library was a source of investigation through reading non-fiction texts, using the index and contents list to find out facts for themselves and to share with their classmates, often producing a glossary display; an alphabet of…topic.

It is interesting to me that the 1987 National Curriculum was a 95% correspondence with that which my and other local schools were doing. It meant small tweaks rather than big alterations.

I am finding the current discussion on the broader curriculum a little stilted at times. There will be significant similarities across time and there will already be a lot of good practice that can be retained.

Topic titles allocated to year groups.

Planning is essential.

Topic details; essential knowledge to be shared; key questions to be explored; resources available within the school or locally. When I was a head, we developed “topic specs” in around 1993.

Link opportunities between the topic and spoken, read and written English, or mathematics; using and applying knowledge from each to benefit the other, making appropriate links.

Timescales allocated and the order of study, to enable learning from earlier topics to impact on subsequent learning.  

Organised into an annual plan, it’s possible to ensure coverage and also sufficient opportunity to explore specifics in depth, knowing that the year was planned.
​
It’s useful to have an end point for each topic area, maybe a small museum, a display, a performance, piece of art, music or drama/movement, with the potential for an audience to provide the spur for higher quality outcomes.
​

​In many ways, it is sad that we have reached a point in our education history where we are having to reinstate that which was already there in many cases. The 2014 curriculum changes were such that elevating maths and English to such heights distorted teacher efforts, in schools and across training providers who have to follow Government expectations. It takes time and effort to develop curriculum, to articulate a school approach, to embed this into daily practice and then to evaluate and refine, with a constant need to revisit when there are new staff who will need support and mentoring.

For interest, here’s my school KS2 science overview from 2004; based on 7.5 hours per week, blocked time to need.
​

In the meantime, while this development is actioned, five years on from the changes, another generation of children passes through the school, potentially fed a diet limited by the school interpretation of it’s needs at that point in time. Data in maths and English define external judgement. If a school feels vulnerable, concentrating on what is measured can seem an appropriate course of action, but is can also lead to a diminished learning opportunity, which, if coupled with a diminished home opportunity can doubly exclude children from wider life opportunities.

There’s much talk of cultural capital. We need to look at life experiences, too…
​
Is showing children pictures the same as being there?

An open book? How do you tell your story?

Do you offer children something to think, talk, read and write about?

It’s been a quiet Christmas break, which is how it is when you get a bit older. It’s usually making sure that younger generations have a good time; that they are fed and clothed and have presents to open. It has been interesting to drop in and out of Twitter to see what’s being discussed. It can be an eye opener, or occasionally a tablet shutter, as views pass that might elicit a type-delete response.

However, recent tweets about the curriculum suggest that Curriculum is the current hot topic, as Ofsted are putting it at the centre of their next round of thinking, and some commentators seemingly jumping on the opportunity to propound their “knowledge rich” agenda, as if it’s a new phenomenon.

My career in teaching started with training at St Luke’s College, Exeter, from 1971-74. Although Plowden was a high-profile element that was the new core of pedagogic reflection, the sharing of knowledge was central to the science course that I started and the Environmental Education course to which I transferred in year 2, providing a broad subject base for Primary, which became my passion.

It was based on knowledge, the interpretation of which into classroom narratives was left to us. We explored “programmed learning”, which was exemplified by exploring the stages of making a cup of tea or a piece of toast. This showed us the essence of embedded knowledge that is assumed in giving instruction or developing a narrative. It made us better “storytellers”; a mixture of substance and exploration. If you think of sharing a book/(his)story with children, their background knowledge inevitably impacts on their understanding of the whole; that’s Hirsch in a sentence.

We talked of challenge in tasking, with the challenge depending on our understanding of the knowledge that the children had already encountered; it was effectively tested through use and application. Within the task, when children encountered difficulty, it highlighted areas that had ether been missed or had not been assimilated effectively, so in-task teaching would occur. There were tremendous similarities to my own education experiences in the 1950/60s. It was also writ large in the available resource materials, such as Nuffield Science 5-13.
​
Knowledge and challenge were intertwined.
​

And, in my school experience as a teacher, it remained so throughout.

I still have a copy of the textbook that underscored my initial training; Environmental Studies, by George Martin and Edward (Ted) Turner, who was the course leader. For those who would wish to claim that knowledge-rich is a new phenomenon, I’d offer them this book, from 1972 as both a starter knowledge across subjects that sought to give an introduction to thinking practically about the world, supplemented in each chapter with an extensive bibliography for extended reading.

The premise of the course was to provide teachers with the background to introduce children into their world through three layers, Investigation and interpretation, communication, inspiration. Over time, this gave rise to my personal mantra of learning challenge as something to think, talk, and write about, leading to presentation, preferably to a known audience.

The course explored the living and non-living world; essentially chemistry, physics and biology with added geology; the past world around us, architectural features, local archaeological sites and using artefacts; rural and urban living, settlement studies, including use of materials for dwellings and other buildings; conservation, especially within an urban settlement; histories, especially from a locality perspective, but also within a national and international perspective. (Ted Turner took as his inspiration the notion of the Renaissance, especially Leonardo da Vinci. That allowed the summer field trip to be to Florence, at a time when it was possible to wander into galleries freely. However we also had to write about the other aspects too; planning how we would use the available resources to offer the broader curriculum.

Mathematics, of measures, counting and data, language, art and music were significant features.
​
It was a good basic starter, to which I later added two part-time Diplomas, one in Environmental Sciences and the second in Language and Reading Development.
​

Every school within which I worked, from 1974 onwards, had curriculum organisation, to differing degrees. Some had simply headings, of topics that had to be covered within each year, others had broad resource materials from which to develop the topic narrative, which was left to the classteacher to develop based on knowledge of their classes.

The 1987 National Curriculum was a 95% match with our existing curriculum; I was a deputy in a First School.
The subsequent Dearing Review gave a 95% correspondence.

When I became a HT in 1990, there was a need to create a firmer base for the curriculum, which could have been described as a little ad-hoc.

We had a mix of planning layers, starting with whole school and year group. This was premised on allocating topics appropriately.

Every topic had a “topic spec”, which was designed by the subject lead, ensuring that the NC expectations were clear, articulating essential knowledge, skills, challenges, available school and locality resources, plus reminders of quality outcome expectations (Level descriptors rewritten as descriptors of child capability).
​
Every teacher received their planning file in July, before a half day of a closure that allowed them to organise their planning thoughts before the summer holiday. A copy came to me as HT, so I knew in July what the next year “learning map” looked like.

The first two weeks were always designated as “getting to know and settling” weeks, with a teacher designed topic. The second Friday was always a closure, half a day given to planning the detail of the next (few) topic(s), including resourcing from school stock. Topics ranged from a week to several weeks, depending on the needs. The interplay of topics with English and maths allowed for topic generated information to be used in writing or to create mathematical opportunity that offered measures, counting leading to data, or shape and space exploration.

Because the year was based around revisiting areas, especially in maths and English, revision of ideas, aka interleaving, was embedded.

In so doing, we had a curriculum with meat, two veg and a good helping of dessert.

It was planned longer term, so that it had substance. It was broad, balanced and relevant, drawing from the locality as much as possible, to fully immerse the children into their community, as well as drawing from wider opportunities; we did take the children on local trips, but also to London, to the British Museum for Greek, Roman or Egyptian exhibitions. However, time was always against us for day trips, with at least two hours each way on a coach and costs getting ever higher. The IWB did allow us to bring a level of experience into classrooms, taking over from the video or CD player.

While “bright ideas” might be imported, these were always evaluated against what was already offered. If they added something, they were incorporated.

It was a cycle of constant improvement, supported by every subject lead having at least a half day with a County inspector to review the school offering as a whole.

The 1997 National Curriculum with the accompanying strategies, did put some of this under strain, especially when we needed to replace experienced staff. It was noticeable that some applicants were used to a narrower diet. However, personalised CPD opportunities, eg shadowing colleagues, allowed insights into expectations. Staffing stability helped with this; we held onto the “tribal memories”… see blog…

The breadth paid off in national testing, too, where English, maths and science scored highly. Every subject was valued, with quality outcomes celebrated throughout the school, with displays or presentations opening learning to others.

The 2014 Primary National Curriculum was always a worry to me, even though I was not school based, but working in ITE and with parents and inclusion. It articulated English and Maths extensively, while others were diminished. Listening to Tim Oates, early in the process, saying that it was designed to be easier to test highlighted an underlying political agenda.

As we are now a couple of days into 2019. Perhaps a chance for reflection and refinement?

I have no problem with a conversation about what children should be exposed to through their school experience. There must be a clear narrative to learning; it is after all, the school’s internal book.

Every subject can be explored by a 2-year old, a 12-year old or a 22-year old. Their ability to interact with the experience will vary widely, from an initial exploratory phase, which I would see as “play”, through to accommodating, reflecting on and reacting to, ever more sophisticated information. We are on a constant journey, carrying with us, at any point, the accumulated wisdom of earlier experiences. So a “knowledge organiser” as our “topic specs” can be seen today, will vary considerably for each age group, and should do so. It should support a developing narrative approach, not become a knowledge dump which an inexperienced practitioner might simply regurgitate.

Order and organisation are key to teaching and learning success, over different timescales.

I would argue that annual plans allowed teachers to ensure coverage while also developing each topic at depth. Colleagues also benefited from collegiate sharing, either one to one or within practical workshops.

At classroom level, each teacher planned in ways that suited them. They were personal diaries, only considered if there were question marks over children’s progress. Classroom teachers are paid to think. They need to think clearly, on multiple layers, always with children and their progress in mind. That’s why it can be tough at times.

When teaching becomes top-down, teachers start to look at what is expected, to second guess what “those above” are looking for. That this has, on occasion been subject to the management or Ofsted rumour mill, can’t be denied; one local school or colleague passing on their tips from their own inspection, so others copy.

To hold to your own course can be challenging, but it is your own school’s journey that’s important.

It’s your narrative, your history, your present.

More important, it’s your children’s narrative, their history and their present.

That’s your data; what you do for them and what they get out of it. It’s a mix of the obvious, the displays and the books, but also their attitudes in school, their capacity to engage in talk with others. It’s a story, based on words, not numbers, so that children can engage with their own developing narratives.

Children’s pleasure in overcoming challenges and learning…led by teachers who enjoy teaching.
​

If modelling thinking is a key element of teaching, why do we appear to remove concrete apparatus when the mathematical concepts start to get more difficult?

Based on an earlier blog: https://chrischiversthinks.weebly.com/blog-thinking-aloud/talking-maths

It would be interesting to know when the concrete apparatus is withdrawn from the teacher explanation repertoire, as this can be seen as only useful for SEN children, yet, used effectively, can enable even more able learners to make connections through very clear visual manipulation. This can be demonstrated through the use of Dienes base 10 material to explore place value and four rules with decimals to three places, using the 1000 block to represent 1.

How do you know what a child is thinking unless you ask them directly to explain something?

We have become used to Talk for Writing, so why not Talk for Maths? If teachers and children engage in learning dialogue, the teacher can get a better view of how the children are thinking and the learners might become more secure in their willingness to have a go, especially when facing novel situations. We also talk of it being ok to make mistakes, especially in the context of Growth Mindset thinking. I would suggest that an openness to dialogue underpins GM, in that a child should be able to share insecurities and to be able to talk through a resolution. Learning to think and talk is an important stage in being able to do so internally, from the scaffolds developed through discussion and manipulation.

The early days of my teaching career were in a school that focused its approach on the work of two key figures in mathematics; it helped that the head was a County adviser for maths, so we also benefitted from regular visits by his colleagues in the inspectorate.

There were two key elements highlighted, logic and modelling mathematical thinking supported by continuous use of structured materials. The work of Zoltan Dienes was central, embodied in the structured approach created by Harold Fletcher, whose workbooks were the spine for mathematical activities by the children. For both, we were given the key background texts to read and understand. In this way, we avoided falling into the trap of just doing the activity booklets, as both the teacher guides and the senior staff accentuated the central place of concrete apparatus. This, in itself, was accentuated through staff training as a group or 1:1 coaching to need.

From https://www.stem.org.uk/elibrary/resource/30000 an extract of Fletcher’s background.

Harold Fletcher was seen as an outstandingly gifted teacher and educationalist. While he was always a firm believer in children being able to calculate accurately, he found from his own teaching that they could achieve remarkable results in other aspects of mathematics. Harold Fletcher considered the mathematics he wanted children to learn under six strands:

Number Pattern Shape Pictorial Representation Measurement Algebraic Relations.

With the help of a team of experienced teachers and educationalists, Harold Fletcher wove these strands into a teaching sequence which was called Mathematics for Schools. Examples of classroom activities are used to describe the mathematics, complete with teacher dialogue, diagrams and outcomes from recording.

Each element of number, addition, subtraction, division and multiplication along with place value was developed showing the use of concrete materials and styles of notation (many of which would be seen later in the Framework for Teaching Mathematics (NNS; National Numeracy Strategy).

​

Shape begins with an introduction to solid shapes before bringing in 2 dimensional or plane shapes. This is followed with measuring, area, capacity and volume before concluding with symmetry and tessellations. As with all aspects of the series it was stressed that concrete materials should still be used.

Pictorial Representation focused on students, from an early age being able to collect information, record it in pictures and most of all, think about it and use it for further number practice. The foundations for graphs were introduced before dealing with them further in Algebraic relationships. A final section on “How can I help my child?” contained some do’s and don’ts. A pdf of a parent guide is available from the STEM site above.

The second key character in my mathematical education as a teacher was Zoltan Pal Dienes (Pal anglicized to Paul). Looking up some detail, I came across his relatively recent obituary.

​

DIENES, Dr. Zoltan Paul Obituary from http://www.zoltandienes.com/obituary/

Age 97, of Wolfville, Nova Scotia, passed away peacefully on January 11, 2014. Zoltan Dienes, internationally renowned mathematician and educator, was both a public figure and a much loved family man.

Zoltan was born in the Austro-Hungarian Empire in 1916, son of Paul and Valeria Dienes. His early years were spent in Hungary, Austria, Italy and France. He always had a fascination with mathematics, even hiding behind a curtain to hear his older brother’s maths lesson, for which he was deemed too young!

At 15 he moved to England. He received his Ph.D. from the University of London in 1939. Zoltan understood the art and aesthetics of mathematics and his passion was to share this with teachers and children alike.

He was fascinated by the difficulties many people had in learning mathematics and wanted others to see the beauty of it as he did. Consequently, he completed an additional degree in psychology in order to better understand thinking processes. He became known for his work in the psychology of mathematics education from which he created the new field of psychomathematics.

Referred to as a “maverick mathematician”, Zoltan introduced revolutionary ideas of learning complex mathematical concepts in fun ways such as games and dance, so that children were often unaware that they were learning mathematics – they were having a wonderful, exciting, creative time and longing for more. He invented the Dienes Multibase Arithmetic Blocks and many other games and materials that embodied mathematical concepts.
​

According to a Montana Mathematics Enthusiast monograph from 2007, “The name of Zoltan P. Dienes stands with those of Jean Piaget and Jerome Bruner as a legendary figure whose theories of learning have left a lasting impression on the field of mathematics education…

Dienes’ notion of embodied knowledge presaged other cognitive scientists who eventually came to recognize the importance of embodied knowledge and situated cognition – where knowledge and abilities are organized around experience as much as they are organized around abstractions. Dienes was an early pioneer in what was later to be called sociocultural perspectives and democratization of learning.”

I had a wry smile when I realised that his initials are ZPD, which is immortalised in the work of Vygotsky as the Zone of Proximal Development, something, I am sure that Dienes would have appreciated.

Conservation of number became a shot topic of conversation on social media during the week. It is, without a doubt an underlying concept in the learning of mathematics, akin to chunking of information to make subsequent thinking and manipulation easier.

Definition
Conservation of numbers means that a person is able to understand that the number of objects remains the same even when rearranged.
What is conservation of number?

• Conservation of number - the logical thinking ability to recognise that the numerical value of an object remains invariant with physical rearrangement - is a fundamental "cognitive milestone" during children's development (Crawford, 2008 p. 1). 
  
  
• The concept of conservation was developed by Jean Piaget during the mid-1900s, who claimed it as "concrete operational" and, therefore, "unattainable" until children are of 7 or 8 years old (Halford & Boyle, 1985, p. 165). 

It is interesting visiting schools and classrooms, watching many numeracy lessons. It is often clear that children are regressing to counting from one, which suggests that they have not reached the conservation stage, even when dealing with relatively small numbers. This might be down to lack of modelling, therefore expectation, with high adult oversight and interaction.

Some of the materials being use for modelling may be less helpful, in that they might encourage children to start counting from one, for security.

Multilink or Unifix blocks are common in early classrooms. Where the mathematics takes children beyond tenness, breaking the chain into ten rods can be useful to accentuate that concept. It is heartbreaking to watch a child count, then have to restart the count because they have been interrupted. Making rods of ten would allow for interruptions and a means of continuity.

For this reason, I still have a preference for Dienes base ten equipment, as it allows early access to models of exchange, creating tens then hundreds. It accentuates place value and, using the function machine conceptualisation allows all four rules of number to be modelled effectively. With a visualiser attached to a class IWB, the modelling can be done on a large scale, enabling more to access. I recognise that in the days before such technology, there were visual limitations to modelling to large groups.

From Maths No Problem, the following accent on concrete apparatus seems to fit with this approach.

Concrete, pictorial, abstract (CPA) is a highly effective approach to teaching that develops a deep and sustainable understanding of maths in pupils. Often referred to as the concrete, representational, abstract framework, CPA was developed by American psychologist Jerome Bruner. It is an essential technique within the Singapore method of teaching maths for mastery.

Recently working with ITE trainees, in the conversation the idea of conceptualisation was raised. Using the simple example of 2+2=4, the trainees were challenged to explore the underlying necessary concepts to have a full grasp of the challenge. Twoness, fourness, addition (including synonyms) and equality, or balance, linked to balanced equations, eg 2+2=3+1. It was an eye opener to some.


​Race to the flat
A very simple activity that can be very effective in supporting rapid calculation could be called race to or from the flat.

As long as you have Dienes base 10 materials and dice, this can be developed to cater for a variety of needs.
The rules of each game are simply described.
·         Decide whether it’s a race to or from the flat (100 square). Decide whether, when the dice are thrown, the numbers are added together (any number of dice) or multiplied (two or three dice?).
·         Dienes materials available to each group, plus dice appropriate to the needs of the group.
·         Each child takes turns to throw the dice and calculate the sum or product.
·         This amount is then taken from the general pile and placed in front of the child. The calculation can be recorded eg 3+4=7. This can provide a second layer of checking.
·         If playing race from the flat, the child starts with ten ten rods, then takes an appropriate amount from these.
·         Subsequent rounds see pieces added to the child’s collection; recorded as needed, eg round 2, 5+2=7 (7+7=14; the teacher should see one ten and four ones)
·         The first child to or from the flat is the winner.
Altering the number of dice alters the challenge.

An extension could be a race to the block (1000 cube), or from the block, each child starts with ten 100 squares. If multi-sided dice, or different numbers of dice are available, the challenge alters yet again.

I came across some notes from some years ago, where I sought to put together examples from Dienes to enable colleagues to utilise the system to support their maths teaching.

Something from my file...
​
A starter for an activity that could be developed in many directions, depending on the needs of the children. Shape and pattern in one activity?

As long as you have Dienes base 10 materials and dice, this can be developed to cater for a variety of needs.
The rules of each game are simply described.
·         Decide whether it’s a race to or from the flat (100 square). Decide whether, when the dice are thrown, the numbers are added together (any number of dice) or multiplied (two or three dice?).
·         Dienes materials available to each group, plus dice appropriate to the needs of the group.
·         Each child takes turns to throw the dice and calculate the sum or product.
·         This amount is then taken from the general pile and placed in front of the child. The calculation can be recorded eg 3+4=7. This can provide a second layer of checking.
·         If playing race from the flat, the child starts with ten ten rods, then takes an appropriate amount from these.
·         Subsequent rounds see pieces added to the child’s collection; recorded as needed, eg round 2, 5+2=7 (7+7=14; the teacher should see one ten and four ones)
·         The first child to or from the flat is the winner.
Altering the number of dice alters the challenge.

An extension could be a race to the block (1000 cube), or from the block, each child starts with ten 100 squares. If multi-sided dice are available, the challenge alters yet again.

With original words by Tony Hatch, Messing about on the River was a song on weekend children’s radio in the early 1960s.

As a child growing up in Brisbane, Qld, and Torbay, boats were a regular feature of life. Being in or on the water was a particular pleasure of growing up, with one darker incident, when a friend and I were the last people to see a boat loaded with six men and several sacks of cockles, with so little draught that while we were still out rowing, the police launch drew alongside and asked us if we’d seen them, as they hadn’t got back as planned. They had shipped water and all six had drowned when their boots, filled with water, had acted as anchors. It led to my first and only appearance in a Coroner’s court.

A tweet today talking of the oral tradition and nursery rhymes, reminded me of an earlier blog, but also made me think a little further about examples from my teaching.

As a teacher of a year 3 class around 1984, the topic choice was water, which provided the science, with exploration of floating and sinking, density exploration, evaporation and the water cycle, especially on showery days, siphons and pumps. Rafts enabled exploration of area and volume, linking science and maths. Rivers underpinned the geography, a visit to the Victory for some history and, for a short period, the song was the basis for dictionary and reference book research.

In the days before mass internet availability, the use of non-fiction books, using the contents and index to seek out information that could then become a general class resource, eg within displays was a common feature. Any parent who was associated with the navy, Royal or merchant, or a sailor or boater might be asked to visit to provide a personal talk.

Occasionally, this developed into an “alphabet of…” whatever was the current topic, creating a glossary of useful terms.

The song gave the focus, with specific words being identified as worthy of exploration. Ultimately, the activity also developed in-class thesaurus-style collections of associated words. By becoming the active explorers, children then often went home and found out more for themselves. The song became the vehicle for broader language development, but also, by being learned by heart for a performance in their assembly, helped with memory.

Oracy is a current buzz word. Like many others, it seems to mean different things to different people. To me, it means giving children something of quality to talk about, in small or larger groups, with the purpose of finding a solution to a problem, or working out how they will tackle a challenge. It’s rarely as formal as a debate, but might become such in specific circumstances. The confidence to interact with peers, to me, is more important than performance to a wider audience, as that’s how we live. Few of us have a soap box upon which to stand or a lectern to hide behind.

Learning to interact verbally is a life skill. A language rich environment encourages that.
​
For those of you who don’t know the song, here’s a link. I'm hoping to resurrect my interest in the water and water activities when retirement beckons... who knows, I may even be tempted to accompany this with singing! 

There’s always a need to fill in a few minutes here and there, even within a well-oiled organisation. You’ve finished and cleared up from a lesson, in readiness for assembly, when a note is circulated to hold on for five minutes while something in the hall is sorted.

You have 30plus children in a snake, ready to walk to assembly and time on your hands.

Poetry can be a great filler. I always had a set of poetry books on the shelf, to share regularly, and could then choose as few or as many as needed to fill in the available time. It’s especially useful if the children know many of the poems my heart, so can join in with the telling, as a rehearsal activity. Children like silly poetry.
​
They also like silly songs, so a collection of these would be developed through the year, so that, with a few minutes and a child chosen, the line could become an impromptu choir, enjoying the feeling of performing together.

Blank playing cards offered a wide range of potential uses.

The numbers 1-100 written on separate cards allowed two or three to be selected at random, with the chosen numbers discussed by the children. This allowed discussion of larger/smaller, or greater/lesser, place values, ordering a set of numbers according to attributes. It could also become random mental maths challenges with addition, subtraction potential.

Dice come in different number combinations. These can be thrown to create random maths problems.
​
I’ve even used the Dienes base 10 material, challenging children to find specific values; 36= 3 tens and 6 ones.

Blank cards can become flash cards, with particular words to be shared regularly, especially after their phonic components have been covered.

This could be extended to broadening vocabulary needs, where a word selected at random is created into a sentence, and improved around the class. This could be subject specific vocabulary, with the need to incorporate other knowledge into the sentence.

I also had three piles of cards, divided into people, places and things. Children would take one card from each pile, then create a story to link the three elements within the time available. This style of activity was occasionally developed as a writing stimulus, for longer consideration.

Images. A classroom collection of images, as paper copies, or through the IWB becomes a talking point, starting from description of what is seen, through speculation about what happened before and after the image was taken, or what was happening outside the frame of the image.

Five minute slots can be very important for rehearsal activities. It is far better to have ideas as a back-up plan, as five minutes can sometimes extend and a line of children standing around can get very restless, developing into a behaviour management issue.

My advice is always to be prepared. Have something up your sleeve, especially if you can do magic tricks!

You might like to look at one minute data ideas or five senses starter activities

​Working with an infant class, I had visited our local materials bank and come back with a large roll of card. Incorporated within another art activity, every child did hand print handspans along the card. This became our non-standard tape measure, which we used to measure (approximately) the circumference of trees in the school grounds and width of the canopy, with an extension of measuring the playground. It became clear that additional organisation was needed, so the roll was divided into sections of ten handspans. The children were able then to use the available resource and some tallying to measure the width and length of the playground using the strips of ten handspans.

The strips also doubled as the border for a display, so had multiple purpose.

We did an experiment with each child using their feet to measure the length and width of the classroom. The results were counted and tallied and, surprise, there was a range of result, which lent themselves to a variety of recording methods; arrow charts, lists, bar charts…

I made up a story about a king who asked a carpenter to make a boat that was one hundred feet long. The carpenter worked diligently, and created the most magnificent boat ever seen. When the king came back he took one look at the boat, admired it’s elegance and then put the carpenter in jail for creating a boat that was too short…

The children had to discuss why the king might be angry. The need for agreed measures was brought up and they all agreed that the king should have left a pattern of his own foot as the unit of measurement. A wider discussion explored the basis for standard measures across everyone and the activities were repeated using metre sticks or tape measures.

Measures were always a significant part of much planning; most Primary topics effectively lend themselves, at some point to being able to measure something, in some form, using standard or non-standard measures. It allows working mathematically out of doors, with the results able to be collated and recorded in a variety of forms appropriate to the needs of the age group, introducing young children to data forms early.
​
So, as a rule of thumb, I’d sometimes fill in odd moments with a bit of measuring. It’s surprising how much pleasure young children get by finding that their bodies are natural measures.

It ain’t what you know, but the way that you use it…

It’s been a bit of a week, probably a good one to go out and buy a hard hat, if you spend any time on Twitter. It wasn’t just raining, it was, on occasion, literally pouring. Bile ducts were seemingly emptied on the heads of a few writers willing to proffer views with were opposite to others; as if people can’t see things in a different light. If it wasn’t knowledge, which it largely was, it’s overtaken by some element of English teaching, but that invariably comes back to children’s lack of knowledge that can be utilised within their oral or written efforts or in their ability to decode the written word.

The two “camps” could be described as those who think they can impart knowledge by sharing a specific body of knowledge, within their classroom teaching and those who seek to develop this knowledge through a variety of linking experiences, including the spoken word.
​
This can sometimes appear to be the divide between (some) Primary and Secondary practitioners, with the extended argument that Primary learning is all discovery and play. That the approach is sometimes different, I wouldn’t want to argue, it can become a moot point, but, in reality, it’s likely that there is more convergence than divergence. Whereas young children “play with ideas” through active engagement and sometimes concrete examples, older children, hopefully, are more able to “play with ideas”, so have greater insights from their developed vocabularies.
​

There was a significant announcement yesterday, 12th July 2016, where the Schools’ Minister, Nick Gibb, announced a £40million budget to embed “Shanghai Maths” into 8000 British Primary schools. This was for textbooks and, we assume, staff training. That this works out at £5000 over apparently four years, or £1250 a year per school, doesn’t seem like a great sum, even on my simple calculations, with training cover somewhere around £170-200 a day.

When I started in teaching, there were sets of textbooks on the shelves; there were dog-eared, scribbled on and torn copies of Alpha and Beta maths. I’ll leave you to guess which were more challenging. The school had introduced Fletcher maths, created by Harold Fletcher. The appropriate teacher’s book for every level, to go with the set of textbooks, was available. The head teacher at the time was also a County advisory teacher for maths, so had good background and also very good access to some of the County inspectors who regularly visited.

A significant aspect of these visits, and the accompanying discussions, was that they would rarely refer to the textbooks, which were a distillation of the underlying concepts that were fully explored within the teacher guides. It was the underlying thinking that mattered, not just getting through the books.

The phenomenon of “getting the books finished” can become a driving force when a textbook is used as the core of a school’s approach to any subject. It means that ensuring coverage trumps children’s understanding, leaving some children with gaps in their learning that they carry into the next phase. This could also now be argued with year based curricula such as we currently have in England.

Mathematics has long been decried as a national need for improvement, and, over the past twenty years, since the National Strategies, has, in many ways become ever narrower in outlook, to become arithmetic, rather than mathematics. Number facility is critical, but the practical aspects of learning can enable the practice and application of number in meaningful ways, leading to broader ideas such as data handling from a real life context.

Reference to the teacher guides for any maths scheme offers insights into the underpinning principles of the mathematics, provides the appropriate vocabulary and avoids the teacher regressing to inappropriate language interpretations which may have derived from their own childhood. Kind teachers can offer metaphors which move a child away from the maths. I can remember as a child being told about the “bottle on the step”, to deal with addition and bridging ten.

Mathematics, to some extent, exists for people to make sense of the need to count things and probably started as some kind of one to one matching system, as a tally or knotting system, allowing herders to keep a track of their flock numbers. Other needs pushed the numbers to a point where groupings, or sets of numbers supported a system of values, based on ten-ness. The incorporation of a zero, from, we are told, Arabic scholars, allowed place values to include the empty set.

Mathematics, as it largely relates to the real world, can be captured within alternative objects, matching one to one, thus allowing groupings for different purposes; 2s,3s,4s,10s, etc. Zoltan Dienes created a multibase system that underpinned the maths curriculum of my second Primary School, again with a County maths advisor as head.

Working from concrete apparatus through drawn models to mental imagery, the children developed a very clear facility with numbers, based on elements such as the function machine idea; capturing the idea of “something happening” to the original number, having passed into the machine. Exploring more challenging ideas with multi-function machines, allowed children to analyse what was going on, so that a 15 times table machine would have three elements, multiply by ten, multiply by five, add the two together. Mental maths was supported by such imagery, but those who needed it could use drawn or concrete imagery. The analytical thinking process was what was important. This was always shared, in a kind of “debrief, or sharing” (I’m sorry, I don’t like the word plenary).

I have to say that this was 1979-82.

Making sense of the development of mathematical thought is an essential precursor to being able to teach it effectively. Counting is not, of itself mathematical. It could be seen as part of mathematical poetry, words that repeat every time one restarts the counting process. Young children can learn the poetry without understanding the concepts. More than, less than, conservation of number, commutative laws, etc, all play a part in the development of understanding.

Young children using multilink for counting need to be moved to more formal systems to be able to explore fully what happens with ten-ness, hundred-ness and so on. Over-reliance on the unitary value of multilink can hinder later thought. Using metre sticks for measuring enables the incorporation of larger numbers, as a carpet of 2 metres 45 centimetres is 245 centimetres long. Children get used to bigger numbers naturally and the “playing with” or rehearsal with numbers is an important means to embed them more firmly.

Mathematics, for most purposes, is a practical skill and should retain that base.

It does become abstract and can incorporate aspects of algebra early, with empty set challenges; () + 6=14, which could be presented as x+6=14, what’s x?

My understanding of Shanghai maths, currently being advocated, is that concrete and mental modelling are central to the process of learning maths, as I have described earlier.

Real understanding, by teachers, should be the baseline for development, so that challenges developed for children are progressive in nature, rather than stand-alone activities, over reasonable timescales, to enable embedding and security. There needs to be reflection of the links between concepts, to be made overt, so that children are not continually learning new things in isolation. The growth and development of the subject should be fundamental elements, layering and revisiting, using earlier experience as the platform for progress, through judicious use of concrete and drawn models. Too often, this style of approach is sidelined for pure number, when understanding, at least of a significant proportion of the class, might be insecure.

So, rather than spend money on textbooks, I’d be an advocate of well-selected apparatus purchase, but with an investment of time in really understanding how the whole is put together and how that impacts on particular year groups, thus creating  a holistic approach to the subject development. This should be repeated regularly, captured in some kind of school handbook and new teachers well-mentored into god ways of working.

Avoid the sparkly worksheets, ban the photocopying of 30 sheets and get children talking maths. Talking allows analysis or diagnosis of need. Heads down over a sheet won’t, unless it is specific to the child.

I can imagine a closure day, or a series of twilights, in the school hall, with apparatus and year-group grids, exploring the use of apparatus in each year group, “passing the baton” to the next year group to explain how they use it. Understanding the whole learning journey also underpins support for children whose learning may be less secure or less complete, ie, those who may have specific learning issues or SEN. This is particularly important in “receiving” schools, who need to have a good awareness of what has gone before, to avoid under-expectation, or to deal with their own over-expectation, leading to “deficit teaching”.

Talk maths, model maths, create lasting images. It’s all in the mind, not in the textbook.

Thinking is free; quality thinking time may need to be bought or allocated. Teaching is a team game. Let's focus on team development, not just the "hero(ine) innovator" maths leader.

Number is, and always has been, an essential aspect of mathematical education. Almost everything can be reduced to numbers in some form, if only counting. "How many ...?" is a question that is regularly asked by children or their parents, with the inevitable counting that ensues. The (cardinal) counting system, based as it is on the simple concept of +1, is a part of the "poetry" of growing up. Parents count to and with their children, as simple counting, or within nursery rhymes or songs; one, two, three, four, five, once I caught a fish alive.

Sometimes, it is extended to the ordinal form, as in first, second, third.

​However, counting, although a baseline element of number, is not the be all and end all of maths, but it is one aspect to which children regress, if they are less secure in developmental stages.

​On entering my first Primary classroom, the maths resources were based on matching and grouping cards, similar to the cotton reel picture below, with many different variations on real objects and clip art pictures, which then had to be matched, as 1:1 correspondence with some kind of counting material, as in picture 2, with the reels removed.

​This exploration and "replacement" of one element with another, is an essential step on the road to more abstract interpretation and manipulation of ideas that have their base in the real world.

​Before moving on, try to estimate how many reels there were, either from the picture or the counters. I wonder how many readers will have automatically counted them?

Grouping the counters into groups of two, three, four, etc allows insights into the broader properties of the number being explored. In this case, 7 groups of 2, 4 groups of 3 and 2 extra, 3 groups of 4 and 2 extra. The properties demonstrate an equality which is fundamental to conservation of number.

Eventually, grouping into tens was reached, beginning then to demonstrate the relative values of a collection of ten and the unitary elements. Once you can "read" the image, the group of ten equates to the number 1 in 10, as long as the learner understands the need for the 0 to signify an "empty set". So far, we have explored 1:1 correspondence through matching, grouping and set theories.

Having established a baseline understanding, the learner has to accommodate the idea that numbers can be manipulated, through what we call the "four rules (or functions in the language of Zoltan Dienes) of number", addition, subtraction, multiplication and division.

​Essentially the learner has to understand that they are effecting a change of state, where the number that you started with is acted upon by an "instruction".

​Addition, already encountered in the counting system, essentially entails the understanding that the original number is being enlarged by a specific amount. this can entail counting on from the "conserved" number, not from 1. If a child regresses to counting from 1 they have not secured conservation of number. 

​Linking the counting element to some kind of number based visual system, like Dienes or Numicon, adds another visual, but this can lead to visual representation, diagrammatic modelling, which can then be transposed to the number system.

​"Greater than, less than, difference between", are all underlying concepts that are explored early in a child's maths experience. Difference between does not need to imply subtraction, but often is presented as such, which can introduce unnecessary complications and potentially remove effective methodologies.   
 

I have not mentioned number lines or 100 squares, or any other systematised supports. These need to be introduced with care, if they are not to add any layers of confusion, that can then cause misconceptions that have to be unpicked. In the attempt to "simplify", especially for struggling learners, it is all too easy to add complexities that confuse, rather than support. 

​In my early classrooms, where "maths resources" may have been picked up during a walk at the beach or the woods, a trip to a charity shop, or some other means of sourcing artefacts or counting supports, improvisation was needed.

​Any form of counting material enabled exploration of arrays, underpinning the commutative law , that 3*4=4*3

​Equally, we sometimes explored square numbers as in the picture below.

​The principle that maths is everywhere is an important one. It should not exist in the purity of the maths lesson, but needs to demonstrate that what is learned in maths has application across many areas of life.

Linked blogs
​Talking maths
Maths everywhere
Show maths, talk maths, draw maths, image maths.
Investigating mathematically
More maths Activities
Quick (one minute) data
The answer is twelve?
Story maths?

Move it, draw it, think it, talk it……
Start small and grow thinking.
​

A couple of months ago, I was asked to lead a training session on feedback in mathematics. I spent some time reflecting on the practicalities of this before accepting, as I could see a number of potential pitfalls and blocks, dependent on the school and individual thinking and working methods.

In the end, I decided to take as a central theme talking maths. This would allow me to explore presentational ideas as well as interactive elements of a lesson.

All thinking about teaching and learning comes back to the learner and the teacher understanding or their needs at a particular point in time, with regard to the specifics of the next steps in teaching. This knowledge should build on their previous experiences, with an overview of prior attainment, both of which will determine the means of sharing the new ideas, links with the prior learning, but also to consider the need to explain and model the new information in the light of individual needs. This modelling might be through concrete apparatus, visual diagrammatic representation or oral modelling, if the learners have secure internal models, which they can manipulate.

It would be interesting to know when the concrete apparatus is withdrawn from the teacher explanation repertoire, as this can be seen as only useful for SEN children, yet, used effectively, can enable even more able learners to make connections through very clear visual manipulation. This was made clear in the training session when I demonstrated the use of Dienes base 10 material to explore place value and four rules with decimals.

How do you know what a child is thinking unless you ask them directly to explain something?

We have become used to Talk for Writing, so why not Talk for Maths? If teachers and children engage in learning dialogue, the teacher can get a better view of how the children are thinking and the learners might become more secure in their willingness to have a go, especially when facing novel situations. We also talk of it being ok to make mistakes, especially in the context of Growth Mindset thinking. I would suggest that an openness to dialogue underpins GM, in that a child should be able to share insecurities and to be able to talk through a resolution. Learning to think and talk is an important stage in being able to do so internally, from the scaffolds developed through discussion and manipulation.

Language is key. Using the correct vocabulary and ensuring that children do so, underpins a mutual understanding, and may require interpretation and linkages to a broad range of synonymous language, to ensure all understand. In my opinion, it is fine for a learner to ask for a reminder. Asking supports Teacher Assessment, in that it might demonstrate a level of insecurity, which needs to be addressed to avoid this getting greater.

Asking a child to explain the steps they would take to solve an equation offers an opportunity for writing instructions, or reportage, but also links with a “Show your working” approach, which I would also advocate. Either way, I’d be looking to have as much information as possible available to review outcomes in the round. It is very easy to see maths as producing right or wrong answers.

Talking the steps and showing your working, with apparatus, written models and written methods, would, for me underpin any investigative approach to understanding a child who may be expressing difficulty.

This should be a teacher level activity, so that any remediation needed, perhaps in the hands of a Teaching Assistant, can be focused to the real needs, rather than assumption. The mathematical thinking of the TA needs to be considered, so that “short cuts” and alternative methods are not deployed to make it seem as if the child is getting it right, when they have underlying issues.

Children should be supported in their confidence throughout, encouraging effort, exploring alternative scaffolds and materials as needed, removing these when they are beginning to show confidence. It is also important to demonstrate the links between the scaffolds, eg number lines, number squares, Numicon, Dienes, so that they can select if need arises.
 
Using the analogy of teacher as storyteller, it is important that children are told the story in such a way that they can see the storyline and the developing detail, as it gets progressively harder. Activity should be accompanied by modelling, in a form that supports each learner’s needs. Articulation, from both teacher and learners should be a high priority, as this provides the insights that guide teacher decisions. Just marking the books can often give false information.

Keep talking mathematically, across all subjects, so that it is clear to learners where it can be used and applied. They must learn that maths is all around us, from an early age. Everything can be counted or measured in some form.

Linked posts
Maths everywhere
Show maths, talk maths, draw maths, image maths.
Investigating mathematically
More maths Activities
Quick (one minute) data
The answer is twelve?
Story maths?
​