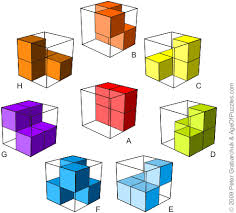
Investigating with cubes
Resource; tray of multilink cubes or similar.
Investigation; To explore how many different shapes can be made with 1,2,3,4,5,6 cubes?
A table of results could be developed, to record results.
A subsidiary activity could be, having created shapes with 4 cubes, better perhaps, if each shape in single colour, to see what shapes can be made by using combinations of cubes, say 12, 20, 28.
This can give rise to drawings of different elevations, top, bottom, four sides. All can lead to mathematical discussions.
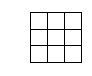
Investigating squares
Repeat this for a square of 4 by 4 squares.
Set out results in a table.
1 square
2 squares
3 squares
4 squares
Is there a pattern in the results? Consider square numbers.
Could you predict how many squares would be in a 5 by 5 grid, then prove it?
How many squares on a chess board?
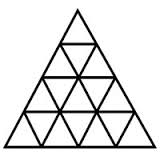
Triangles
In the same way as the squares investigation, the use of triangles might give rise to a different range of mathematical discussions.
Start with one triangle side, two, three, four, etc, so that investigation is ordered, and have the children create a table for results.
After three, they can start to predict how many triangles they expect to find and to explain their thinking.
Pyramids
Using multilink, can you make a square based pyramid two stories high, with one cube at the top?
Three, four, five…
Enables early discussion of square numbers.
Predict the next series of layers, then prove.
Back to one…
Dividing by 2 practice.
Allow each child to choose a starter number, appropriate to their current awareness.
Rules of the task.
If it can be divided by 2, do it, if not, add 1.
Example
33+1=34/2=17+1=18/2=9+1=10/2=5+1=6/2=3+1=4/2=2/ (2=1) repeats
If this is drawn out, linking all the numbers, a tree starts to grow.
Rectangle arrays.
Discuss the attributes of a rectangle.
What’s the smallest rectangle you can make with cubes?
Make a series of rectangles of different sizes and explain their attributes.
How many different rectangles can you make using 12 cubes each? (4)
How many cubes would it take to make five different rectangles with the same number of cubes in each? (36)
Question; is a square a rectangle?
Six (60), seven (120-192), eight (120)
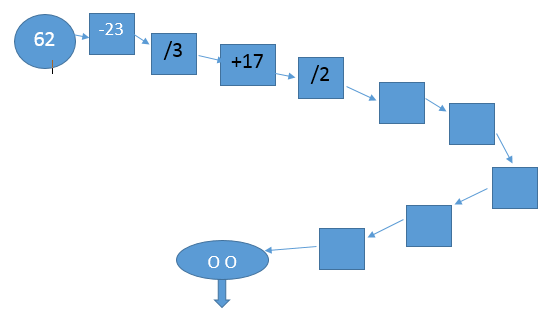
Back to zero “snake”
Based on the idea of function machines, each stage is an equation, with the output becoming the input into the next machine.
The start number can be any with which the child feels comfortable. NB The function machines can be hand drawn, as the task progresses, or before starting, if a specific number of equations are expected.
The child can devise their own trail through the snake, taking responsibility for accuracy. If, say, 20 functions are expected, then it is possible to specify that 4 will be +, 4 as -, 4 as * and 4 as /.
The level of challenge can be differentiated, by expecting somewhere in the snake for numbers to go above a specific point.
Whatever happens through the snake, the answer at the “head” is always zero.
This activity is very simple to organise, but can be adapted to any age and ability, by varying the expectations.
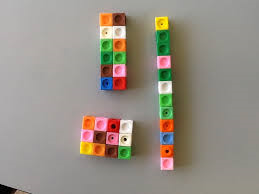
 RSS Feed
RSS Feed
