 |  |
Field geometry?
Looking for simple challenges for children to use outdoors that have links to wider learning, straight lines and circles come to mind.
Challenges:
Lines
Using only three poles and either chalk or cones, can you create a straight line between two points on the playground or field?
Lines can be extended to drawing other geometric shapes. How about exploring Pythagoras theorem? It’s possible with year six. Linking squares with triangles and maybe extending to right angles and building with such simple geometry; builders 3,4,5 triangle?
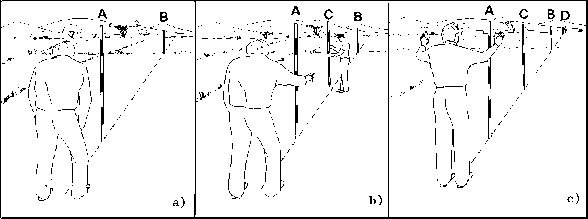
Can you devise a method for drawing a vertical line? Crib note plumb line, a weight on a string.
Circles
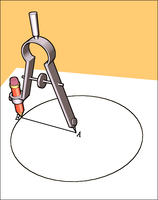
You have a piece of string and a piece of chalk. Devise a way to draw a circle on the playground; for older children, that has a radius of 50cm.
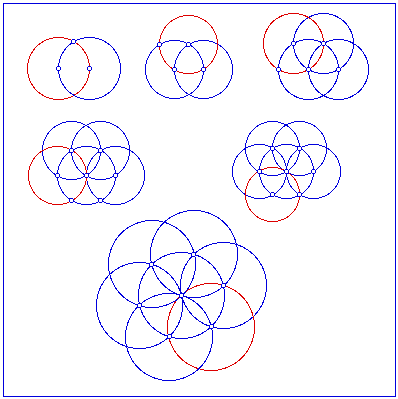
What happens if you have drawn a circle, then “walked” the chalk radius around the circumference and marked points? What shape would it make? How else can a circle be divided?
What happens if you draw a straight line, then draw circles at 20cm points along the line? Play with shapes?
All these challenges could be replicated on a smaller scale with a compass, a ruler and pencils, exploring shapes within circles.
Make windmills?
This exercise was a part of a topic that I did around 1984, with a year six class, looking at energy, so it has some current resonance. Wind and water energies were exemplified and explored through a visit to a local windmill and watermill. Within the DT curriculum, attempts were made to create working models.
Alongside that, exploring circles allowed a homework project to create wind “turbines” that became the focus for a fair test to find the most efficient. The testing was relatively simple, with each turbine mounted on a compass, on a pencil embedded in the ground.
Of course, just making our own windmill, coloured in, could be an interesting task in itself.
This exercise was a part of a topic that I did around 1984, with a year six class, looking at energy, so it has some current resonance. Wind and water energies were exemplified and explored through a visit to a local windmill and watermill. Within the DT curriculum, attempts were made to create working models.
Alongside that, exploring circles allowed a homework project to create wind “turbines” that became the focus for a fair test to find the most efficient. The testing was relatively simple, with each turbine mounted on a compass, on a pencil embedded in the ground.
Of course, just making our own windmill, coloured in, could be an interesting task in itself.
 |  |  |
RSS Feed
