Sometimes, it is extended to the ordinal form, as in first, second, third.
However, counting, although a baseline element of number, is not the be all and end all of maths, but it is one aspect to which children regress, if they are less secure in developmental stages.
On entering my first Primary classroom, the maths resources were based on matching and grouping cards, similar to the cotton reel picture below, with many different variations on real objects and clip art pictures, which then had to be matched, as 1:1 correspondence with some kind of counting material, as in picture 2, with the reels removed.
This exploration and "replacement" of one element with another, is an essential step on the road to more abstract interpretation and manipulation of ideas that have their base in the real world.
Before moving on, try to estimate how many reels there were, either from the picture or the counters. I wonder how many readers will have automatically counted them?
Essentially the learner has to understand that they are effecting a change of state, where the number that you started with is acted upon by an "instruction".
Addition, already encountered in the counting system, essentially entails the understanding that the original number is being enlarged by a specific amount. this can entail counting on from the "conserved" number, not from 1. If a child regresses to counting from 1 they have not secured conservation of number.
Linking the counting element to some kind of number based visual system, like Dienes or Numicon, adds another visual, but this can lead to visual representation, diagrammatic modelling, which can then be transposed to the number system.
"Greater than, less than, difference between", are all underlying concepts that are explored early in a child's maths experience. Difference between does not need to imply subtraction, but often is presented as such, which can introduce unnecessary complications and potentially remove effective methodologies.
In my early classrooms, where "maths resources" may have been picked up during a walk at the beach or the woods, a trip to a charity shop, or some other means of sourcing artefacts or counting supports, improvisation was needed.
Any form of counting material enabled exploration of arrays, underpinning the commutative law , that 3*4=4*3
Equally, we sometimes explored square numbers as in the picture below.
The principle that maths is everywhere is an important one. It should not exist in the purity of the maths lesson, but needs to demonstrate that what is learned in maths has application across many areas of life.











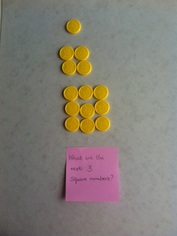
 RSS Feed
RSS Feed
