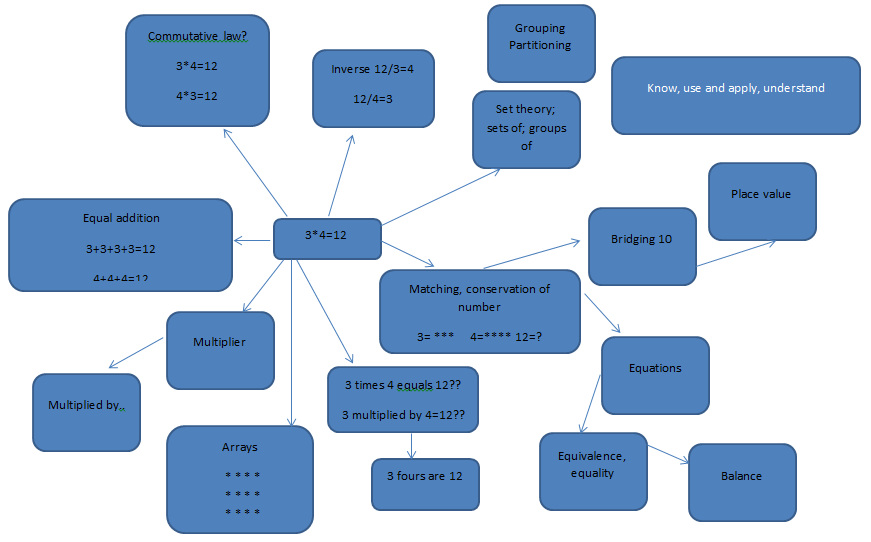
It has to be considered that just rote learning of mathematical formulae may not in itself be productive. The rapid recall of something is good, if one has a use for it. The formula when applied correctly in a situation where its application facilitates the resolution of a problem has merit, especially if recalled rapidly.
I really enjoy driving in France and somehow “enjoy” the mental activity of converting kilometres into miles, so I am able to divide by eight and multiply by five in my head. Useful in that context, as then I can also estimate time of arrival, which, if heading for a meeting can be essential. So perhaps my mental facilities have been honed through use and purposeful application, not just rote and exercise based? Or did I have a talent for numbers? I do remember classmates not finding the learning as easy.
An anecdote from my classroom career comes from a tables chanting session I became aware of a sound that was clearly not the words expected. Moving around the class identified one child who was somehow getting by with “Da, da,de da; da da de da; da da de da de da; da da de da da”, as if she knew the rhythm, but not the words.
Children need to be able to see applications for the factual aspects of learning, so that they can use their energies positively. They also need to be able to identify points where their knowledge needs to be developed. All learning should be within meaningful contexts, with links between ideas being constantly made. Learning becomes deeper through application.
Rote learning can appear to be real learning, but in reality it can be an over-simplification, taking the end product of thinking, putting it in a higher place than is useful to subsequent learning, in so doing creating the illusion of a house of cards.
My mathematics began to falter at “A” level, pure maths, in part because the arithmetic approach did not always support the thinking needed within more abstract number contexts, such as differential calculus. I just couldn’t “see” what was happening. I was fine with formulae applied in sciences, as the purposes were defined.
My current worry is that that the proposals within the draft NC focus more heavily on memory, with fewer overt statements about use and application. Without the latter, there may be many learners whose progress through mathematics reaches personal limits. Are they to be classed as “failures” at that point, or will enlightened teachers still teach in ways that ensure they enlighten children through purposeful and developmental activity?
 RSS Feed
RSS Feed
